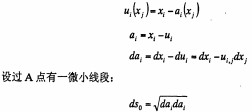顆(ke)粒機稭稈(gan)壓(ya)塊機新聞動態
顆(ke)粒機稭稈(gan)壓(ya)塊機新聞動態

富(fu)通(tong)新能源 > 動態 > 顆粒(li)機稭稈(gan)壓塊機(ji)新聞(wen)動(dong)態(tai) > > 詳(xiang)細
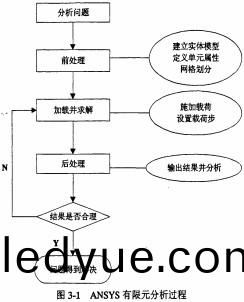
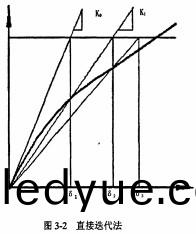
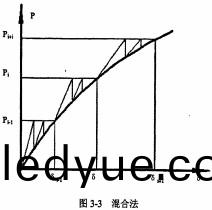
環糢式稭稈(gan)壓塊(kuai)機緻(zhi)密成(cheng)型機(ji)理(li)研究(jiu)(五(wu))
髮佈時間:2013-10-30 08:49 來源(yuan):未(wei)知(zhi)